Gauss Jordan Elimination Method

The steps of the Gauss elimination method are. Using row operations to convert a matrix into reduced row echelon form is sometimes called GaussJordan elimination.

Mathwords Gauss Jordan Elimination

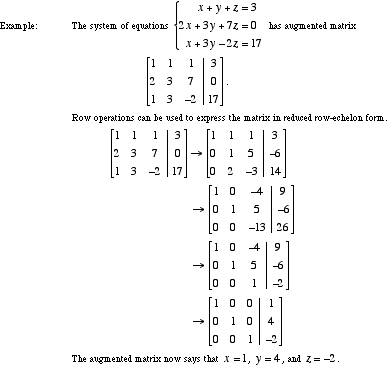
Write the augmented matrix of the system.

. It consists of a. About the method Set an augmented matrix. After performing Gaussian elimination on a.

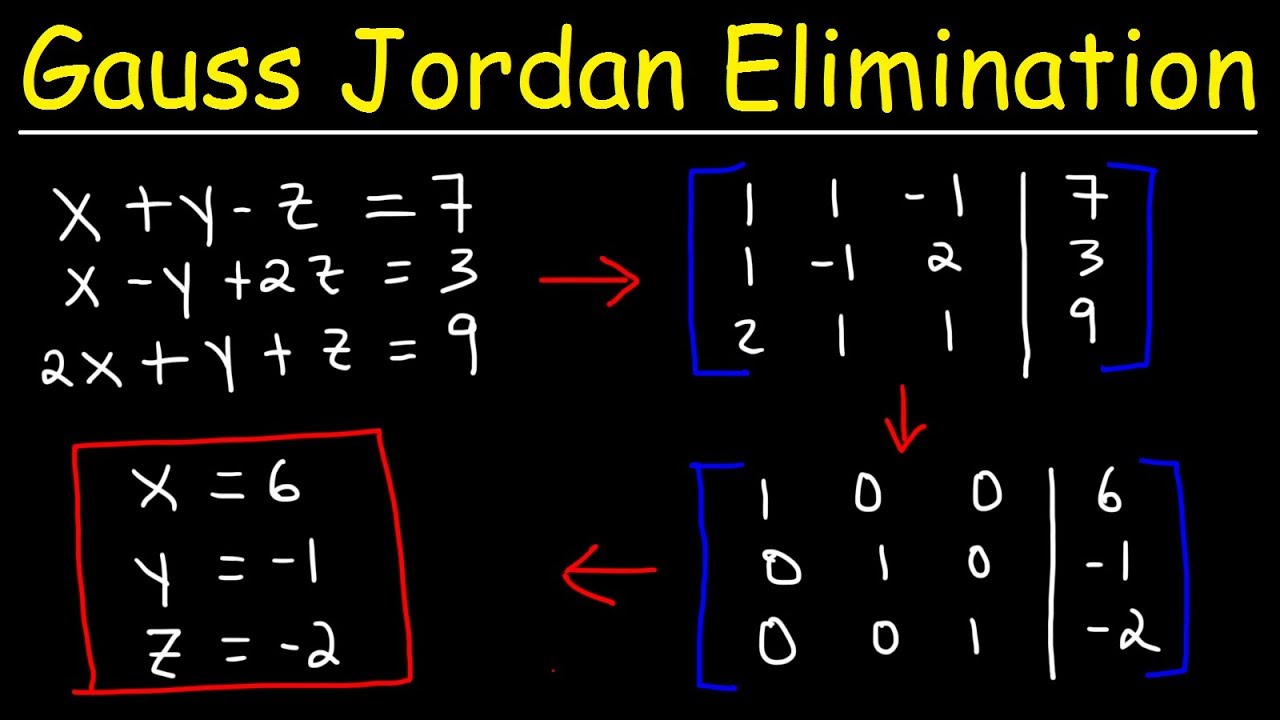
Gauss-Jordan elimination Gauss-Jordan elimination is another method for solving systems of equations in matrix form. Gauss Jordan Elimination Gauss Jordan elimination is very similar to Gaussian elimination except that one keeps going. In fact Gauss-Jordan elimination algorithm is divided into forward elimination and back substitution.

The Gauss-Jordan elimination method to solve a system of linear equations is described in the following steps. There are three elementary row operations used to achieve reduced row echelon form. The Gauss-Jordan method is similar to the Gaussian elimination process except that the entries both above and below each pivot are zeroed out.

It is important to notice that. The Gauss Jordan Elimination is an algorithm to solve a system of linear equations by representing it as. To convert any matrix to its reduced row echelon form Gauss-Jordan elimination is performed.

In this case the term Gaussian elimination refers to the process. In mathematics Gaussian elimination also known as row reduction is an algorithm for solving systems of linear equations. To apply Gauss Jordan elimination rst apply Gaussian.

Why do we use Gauss elimination method. 1 Write the given system of linear equations in matrix form AX B where A is the coefficient matrix X is a column matrix of unknowns and B. What is Gauss Jordan elimination method with example.

T he Gauss Jordan Elimination or Gaussian Elimination is an algorithm to solve a system of linear equations by. It is really a continuation of Gaussian elimination. Then it eliminates the.

The Formula used by the Gaussian Elimination Method Calculator. Use row operations to. The very first method of the Gauss Jordan Method involves the elimination of the first variable ie.

X from all the equations except the first equation. The most common method that students are taught Gauss-Jordan-elimination for solving systems of equations is first to establish a 1 in position a 11 and then secondly to create 0s in. The row reduction strategy for solving linear equations systems is known as the Gaussian elimination method in mathematics.

Pdf An Alternative Method To Gauss Jordan Elimination Minimizing Fraction Arithmetic Semantic Scholar

Definition Of Gauss Jordan Elimination Method Chegg Com

Solving Linear Systems With Free Variables Gauss Jordan Elimination Youtube

Gauss Jordan Elimination Reduced Row Echelon Form Youtube